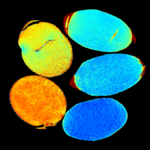
We are making available a MATLAB implementation of a machine learning algorithm for rapidly learning the optimal sampling pattern for MRI.

The left panels show the averaged error map in k-space, with brighter areas indicating larger errors. The error map guides the machine learning algorithm to iteratively optimize the distribution of k-space points, resulting in a lower-error sampling patters, shown in the right panels. For example, staring with the Poisson disc, shown in top left, BASS learns the optimized sampling pattern shown in bottom right.
In a related publication cited below, we propose a new learning algorithm for learning an efficacious sampling pattern in accelerated parallel MRI. The approach, called bias-accelerated subset selection (BASS), is applicable when two conditions are met:
- A set of fully sampled Cartesian k-space data of specific anatomy is available for training;
- An image reconstruction for undersampled data or a direct k-space recovery method for parallel MRI that allows a free choice of the sampling pattern is used.
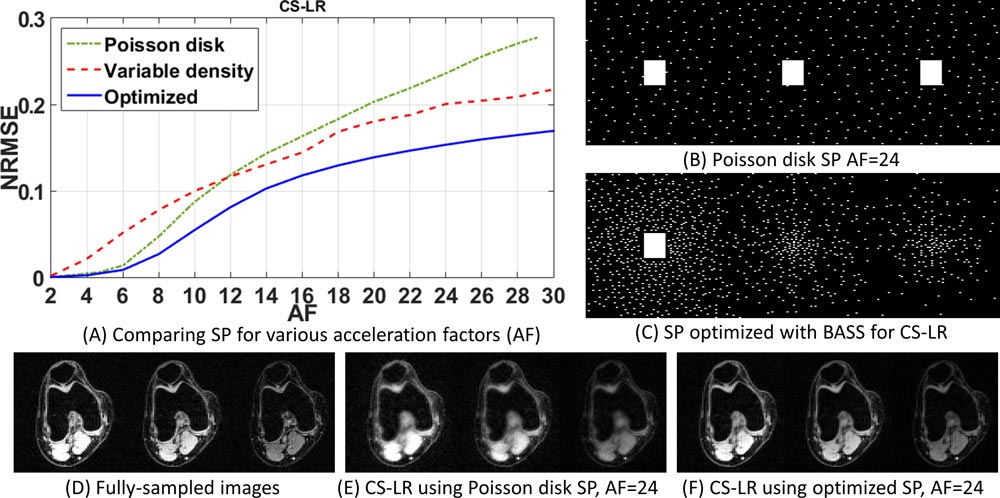
The learned sampling pattern allows fast data collection by capturing the key learned data that result in minor deterioration of reconstruction quality. Our proposed approach has a low computational cost and fast convergence, enabling the use of large datasets to optimize large sampling patterns—important features in high-resolution 3D-MRI, quantitative MRI, and dynamic MRI applications. In the related publication, we describe four parallel MRI reconstruction methods based on low-rankness and sparsity, each used with two different datasets. Our findings indicate that the sampling pattern learned by our method results in scan time nearly twice as fast as that obtained with variable density and Poisson disk sampling pattern for the same level of error.
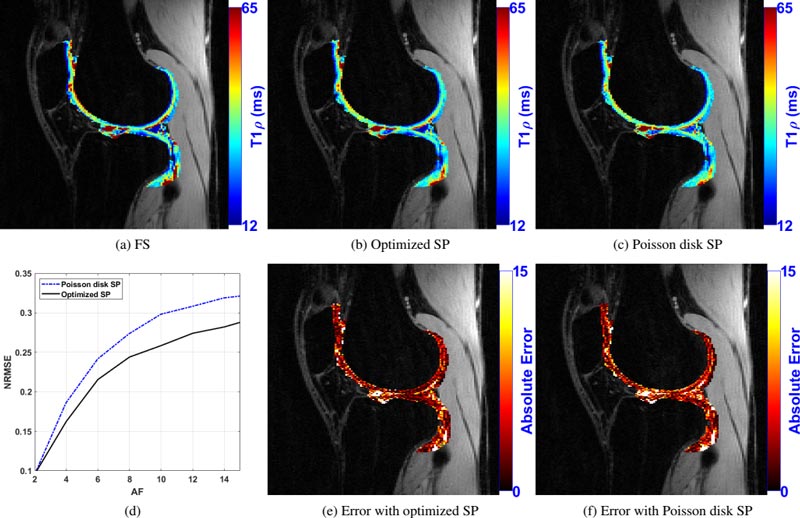
Bottom row, from left: (d) plots of the normalized root mean square error (NRMSE) against acceleration factors (AF) 2-15 for poisson disk SP (blue line) and optimized SP (black line); (e) point-wise error difference between a fully sampled T1ρ map and a map obtained with the optimized SP; (f) point-wise error difference between a fully sampled T1ρ map and a map obtained with the Poisson disk SP.
Related Publication
Fast data-driven learning of parallel MRI sampling patterns for large scale problems.
Sci. Rep. 11, 19312 (2021). doi:10.1038/s41598-021-97995-w
Please cite this work if you are using data-driven learning of MRI sampling pattern in your research.
References
Monotone FISTA with variable acceleration for compressed sensing magnetic resonance imaging.
EEE Trans. Comput. Imaging. vol. 5, no. 1, pp. 109–119, Mar. 2019. doi: 10.1109/TCI.2018.2882681
fastMRI: An open dataset and benchmarks for accelerated MRI.
arXiv. 21 Nov. 2018. arXiv:1811.08839
Data-driven design of the sampling pattern for compressed sensing and low rank reconstructions on parallel MRI of human knee joint.
ISMRM Workshop on Data Sampling & Image Reconstruction, 2020.
Fast Data-Driven Learning of MRI Sampling Pattern for Large Scale Problems.
arXiv. 4 Nov. 2020. arXiv:2011.02322
Get the Code
The software available on this page is provided free of charge and comes without any warranty. CAI²R and NYU Grossman School of Medicine do not take any liability for problems or damage of any kind resulting from the use of the files provided. Operation of the software is solely at the user’s own risk. The software developments provided are not medical products and must not be used for making diagnostic decisions.
The software is provided for non-commercial, academic use only. Usage or distribution of the software for commercial purpose is prohibited. All rights belong to the author (Marcelo Wust Zibetti) and NYU Grossman School of Medicine. If you use the software for academic work, please give credit to the author in publications and cite the related publications.
Version History
| Version | Release Date | Changes |
|---|---|---|
CAI2R_DDLSP_web_reduced_V3.zip [655.4 MB] | 2020-09-30 | Version used for the study published in Nature Scientific Reports (see related publication, above). |
CAI2R_DDLSP_web_V3.zip [2.9 GB] | 2020-11-06 | Version used for the arXiv preprint (see references, above). |
Contact
Questions about this resource may be directed to Marcelo Wust Zibetti, PhD.
Related Story
Marcelo Zibetti, imaging scientist at NYU Langone Health, talks about efficiency in MRI, the value of differing vantage points, and learning by thinking across disciplines.
Related Resources
MATLAB scripts for learned pulse sequence parameters of magnetization-prepared gradient echo sequences used in multi-component T2 and T1ρ mapping.
MATLAB scripts for data-driven optimization of magnetization-prepared gradient echo sequences used in T1ρ mapping.
Simultaneous machine learning optimization of parallel MRI sampling pattern and variational-network image reconstruction parameters.
An accurate, rapidly converging, low-compute algorithm for approximating solutions to the least absolute shrinkage and selection operator (LASSO) problem.