We are sharing a MATLAB implementation of a machine learning algorithm for learning an optimized k-space sampling pattern in parallel MRI while also learning the parameters of a variational network used to reconstruct MR images.

The joint learning approach identifies effective pairs of k-space sampling locations and reconstruction parameters, resulting in better images than those reconstructed with conventional sampling patterns.
In experiments, combined learning has yielded observably improved images and better metrics of image quality. Improvements in root mean squared error (RMSE), structural similarity index measure (SSIM), peak signal-to-noise ratio (PSNR), and high frequency error norm (HFEN) have ranged from 1 percent to 62 percent. For more details about the advantages of this approach, see the related publication below.
To learn the sampling pattern, our code employs an algorithm called bias-accelerated subset selection (BASS, available for download as Data-Driven Learning of MRI Sampling Pattern). To learn the variational network parameters, our code employs Adam, an algorithm for stochastic gradient-based optimization. For more information about these methods, see the references below.
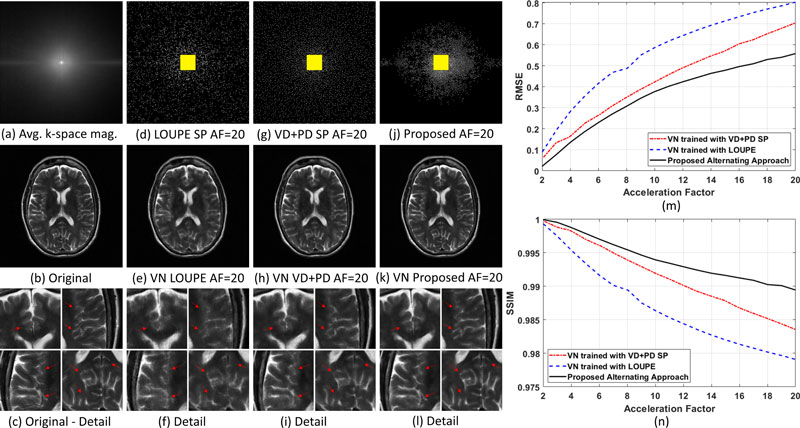
In the first column on the left, from the top: (a) shows the average of the k-space magnitude in the training dataset, (b) shows the original reference image, and (c) shows four areas of detail (arrows point to the most relevant differences across reconstructed images). The second column (d)-(f) shows the sampling pattern, reference image, and areas of detail for a method called LOUPE, short for Learning-based Optimization of Undersampling Pattern (RMSE=0.79). The third column (g)-(i) shows the pattern, image, and detail for a variable-density and Poisson-disc (VD+PD) SP (RMSE=0.70). The last column (j)-(l) shows the pattern, image, and detail for the proposed combined learning approach (RMSE=0.55).
On the right, graph (m) plots RMSE (lower is better) of the three methods against acceleration factors; graph (n) plots SSIM (higher is better); the benchmark for each metric is the original reference image.

This illustration shows that the machine learning algorithm has learned to exploit complex-conjugated symmetry of k-space acquisitions, such as half-Fourier or partial-Fourier. The sampling density of the SP decreases from the center outward, indicating that the algorithm has learned variable density. Spacing between samples is highly regular, increasing outwardly from the center, indicating that the algorithm has learned the importance of such spacing, which is a characteristic of the Poisson-disc and VD+PD sampling patterns.
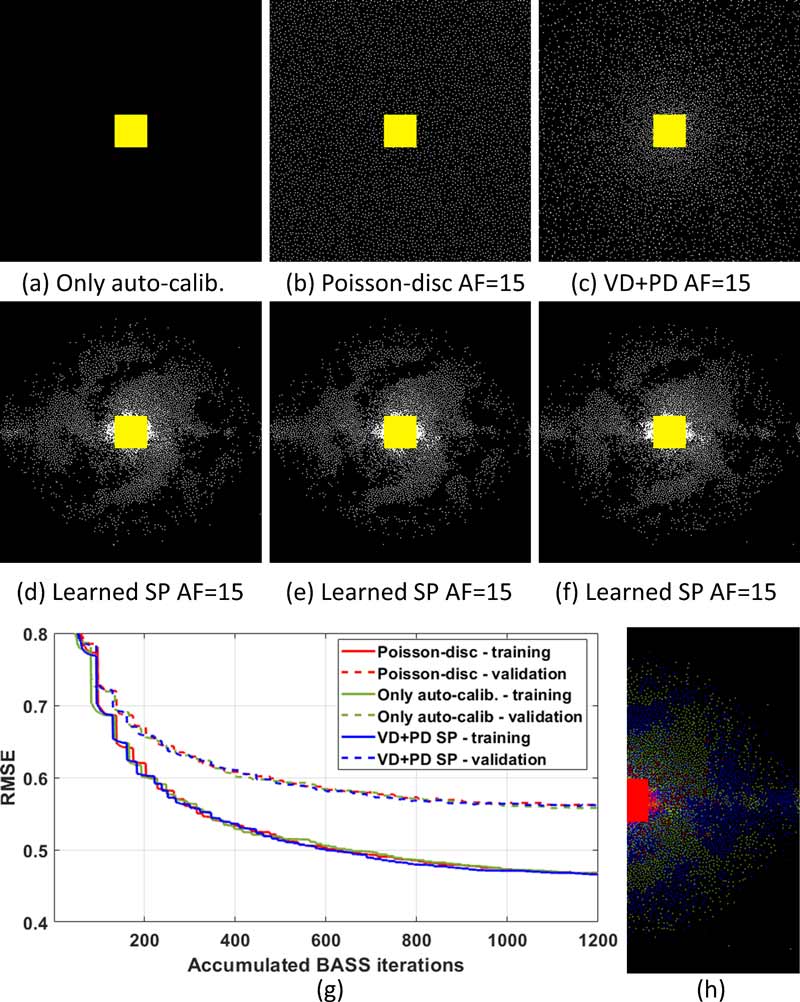
From left, the initial sampling patterns for (a) an empty SP with only the fixed auto-calibration area in yellow, (b) a Poisson-disc SP, and (c) a variable density and Poisson-disk (VD+PD) SP; corresponding learned SPs are shown in (d), (e), and (f), respectively.
Graph (g) plots the RMSE over accumulated iterations of bias-accelerated subset selection (BASS).
In (h) we illustrate some aspects of the position of the samples in the learned SP: the original positions of the left-hand side of the learned SP appear in green; samples projected from the negative side of the spectrum (equivalent to horizontal and vertical flipping) appear in blue; coincident samples appear in red.
Related Publication
Alternating Learning Approach for Variational Networks and Undersampling Pattern in Parallel MRI Applications.
IEEE Trans Comput Imaging. 2022 May;8():449-461. doi: 10.1109/TCI.2022.3176129
Please cite this work if you are using data-driven learning of MRI sampling pattern in your research.
References
Alternating Learning Approach for Variational Networks and Undersampling Pattern in Parallel MRI Applications.
arXiv. Preprint posted online October 27, 2021. arXiv:2110.14703 [eess.IV]
Monotone FISTA with Variable Acceleration for Compressed Sensing Magnetic Resonance Imaging.
IEEE Trans Comput Imaging. 2019 Mar;5(1):109-119. doi: 10.1109/TCI.2018.2882681
fastMRI: An Open Dataset and Benchmarks for Accelerated MRI.
arXiv. Preprint posted online November 21, 2018. arXiv:1811.08839 [cs.SV]
Fast data-driven learning of parallel MRI sampling patterns for large scale problems.
Sci Rep. 2021;11(1):19312. doi: 10.1038/s41598-021-97995-w
Fast Data-Driven Learning of MRI Sampling Pattern for Large Scale Problems.
arXiv. Preprint posted online November 4, 2020. arXiv:2011.02322 [eess.SP]
Adam: A Method for Stochastic Optimization.
arXiv. Preprint posted online December 22, 2014. arXiv:1412.6980 [cs.LG]
Get the Code
The software available on this page is provided free of charge and comes without any warranty. CAI²R and NYU Grossman School of Medicine do not take any liability for problems or damage of any kind resulting from the use of the files provided. Operation of the software is solely at the user’s own risk. The software developments provided are not medical products and must not be used for making diagnostic decisions.
The software is provided for non-commercial, academic use only. Usage or distribution of the software for commercial purpose is prohibited. All rights belong to the author (Marcelo Wust Zibetti) and NYU Grossman School of Medicine. If you use the software for academic work, please give credit to the author in publications and cite the related publications.
Version History
| Version | Release Date | Changes |
|---|---|---|
CAI2R_DDL_SP_VN.zip [1.5 GB] | 2022-05-17 | Version used for the published IEEE-TCI paper (reference pending). Includes VN and UNET reconstructions. Includes monotone and non-monotone BASS. |
CAI2R_DDL_SP_VN.zip [1.22 GB] | 2022-01-14 | Version used for the arXiv preprint cited above. |
Contact
Questions about this resource may be directed to Marcelo Wust Zibetti, PhD.
Related Story
Marcelo Zibetti, imaging scientist at NYU Langone Health, talks about efficiency in MRI, the value of differing vantage points, and learning by thinking across disciplines.
Related Resources
MATLAB scripts for learned pulse sequence parameters of magnetization-prepared gradient echo sequences used in multi-component T2 and T1ρ mapping.
MATLAB scripts for data-driven optimization of magnetization-prepared gradient echo sequences used in T1ρ mapping.
Machine learning optimization of k-space sampling for accelerated MRI.
An accurate, rapidly converging, low-compute algorithm for approximating solutions to the least absolute shrinkage and selection operator (LASSO) problem.